20.2 Developing Problem-Solving
Skill
Two definitions of "problem"
are "a source of difficulty or trouble" and (as it is used in this
section) "a question proposed for solution or discussion." Most
people enjoy the stimulating challenge of a good problem and the satisfaction
of solving it. You will feel this satisfaction more often when you
master the tools of problem solving.
Get a Good Start by Understanding
the Problem
Get "oriented" by using
all available information (words, pictures, and free) to form a clear, complete
mental picture of the problem situation: what is happening, and what are the
questions? Like a good detective, be aware of what is in plain view and
aggressively search for clues.
WORDS: Read the problem statement
carefully, to get accurate comprehension. Study the word meaning
and sentence structure, to gather all of the important facts. Most
problems are written clearly; the problem-writer isn't trying to mislead you,
so just use standard reading techniques to accurately interpret what is written.
You will probably find it useful to "skim" a problem to get an overview,
and then re-read it carefully for details, using the "successive refinements"
method that is described in more detail later.
Occasionally a problem contains useless information
— a "decoy". In Section 3.3, Problem 3-A shows how decoys "give
you practice in deciding relevance, so you can learn to recognize what information
should be used and what should be ignored." { note: Section
20.2 is from the final chapter of Physics: Tools for Problem Solving, a
supplementary textbook for introductory college physics that I wrote in the
late 1980s. Occasionally I'll refer to ideas in Chapters 1-19 of this
book, such as "Section 3.3" above. }
PICTURES: If there is a diagram,
study it. Or make your own picture; when the problem information (lengths,
angles, forces, velocity,...) is visually organized on paper, it is easier to
understand. This also decreases your memory load, leaving your mind free
to do creative thinking.
Section 3.4 discusses how tvvax tables and force diagrams help
you translate information between thinking modes [words, pictures, equations]
and recommends that you treat drawing as a thinking tool, not as art.
{ note: I first read about "modes of thinking" in Conceptual
Blockbusting by James Adams. Later, I adapted and applied this idea
to problem solving in physics. }
FREE INFORMATION: The problem-writer
may expect you to assume certain reasonable things about the problem situation,
or to use data that isn't "given" in the problem but is available
in textbook tables or in a special part of the exam.
Planning and Action
Here is a simple but useful model
of problem-solving strategy.
1) Orientation: As described
above, translate the problem's words, pictures and free information into a clear
idea of NOW (the situation that is defined by the problem-statement) and GOAL
(what the problem is asking you to do).
2) Planning: Figure out how
to get from where you are NOW to the GOAL.
3) Action: Start doing your
plan, and continue until you've reached the goal.
4) Check: Ask yourself, "Have
I answered the questions that were asked? Have I reached the GOAL?"
After orientation you may be able to plan the entire solution from NOW to the GOAL. It is often useful, however, to plan in stages by looking for a point where you can say "After I get to here, the rest of the way will be easy." This halfway point is a subgoal. Here is a summary of the overall strategy:
Step 2: Plan a subgoal — "If I can get to here, I'll be able to reach the goal."
Step 3: Do it — first reach the subgoal, then continue on to the goal.
| 1 NOW |
----> 3 |
sub-GOAL |
----> ----> 3 |
GOAL |
Try to keep sub-problems and the
overall problem in your mind at the same time, and make smooth transitions
between these levels. If you can say "after I do this step I'll know
__ and then I can do __", it is easier to plan overall strategy, because
you won't "miss the forest while you're busy looking at the trees."
A closely related strategy is go-and-improvise.
After orientation, start doing something productive, anything that looks like
it might be useful (ask yourself "What can I do with what I know?")
until you reach a point where a solution plan becomes clear. { If
you discover how the problem fits into a familiar pattern, the solution is easy.
Here's an example travelers will recognize. During a trip north on Interstate
5 from Los Angeles to Seattle, you stop to eat dinner in an Oregon city and
get lost. But while driving around the city you see an "I-5 North"
sign, and you can suddenly say "I'm not lost anymore. Now I know
what to do!" }
Pattern Recognition
When you ask a computer to find
a certain phrase in a word processing file, it searches through the file until
it finds a "match." This strategy can also be used for solving
problems: form a clear mental image of the problem situation, then search your
memory for a match. Most problems are variations of previous problems,
not duplicates, so it is rare to find a "whole problem" match.
Instead, look for matches at the level of principles, equations and sub-problems.
Then use these individual tools, modified in whatever way is needed to solve
the present problem.
Your pattern-recognizing skill will improve
as you do more problems and as you learn to focus your attention on the relevant
aspects of a problem situation. Consider three motions: a rock-on-a-string
moves in a circle, tire friction lets a car drive around a circular track, and
gravity makes the earth orbit around the sun. If you focus on the obvious
differences, you'll miss an important similarity — each motion is circular.
This means that you can, as described in Section 5.2, use the same basic equations
for all three situations.
You should know the range of usefulness and
the limitations of each physics tool. For example, every equation has
" if... then..." conditions and "cues" that tell you
when the equation can (and cannot) be used. Good problem solvers generalize
an equation to all appropriate situations: no more, no less. Over-generalization
will make you use the equation when you shouldn't, and you'll get an incorrect
solution. But with under-generalization you
won't recognize a situation where the equation is needed, and you'll get no
solution.
How to develop skill in
solution-planning
TOOLS: You must be
able to understand physics principles, translate between thinking modes (words,
pictures, equations), perform mathematical operations (as summarized in Chapter
18), know each equation (cues for when it can be used, its links, the physical
meaning of each letter), and use problem-solving strategies. These tools
are emphasized throughout the first 19 chapters of this textbook.
Your skill in solving problems will depend
on whether you can use these tools quickly and easily (to free your mind for
creative planning), reliably (with minimum error) and flexibly (in a wide variety
of problem situations).
MEMORY AND EXPERIENCE: To use tools intuitively you must "internalize" them by working to develop an active memory, and learning from experience like the welder and basketball player in Section 20.1. With practice, you will get better at planning complex multi-step solutions, and you'll be more comfortable when you must "improvise as you go."
ATTITUDE:
Your problem solving is more effective — and more fun — when you have a positive
attitude. Attack each problem with enthusiasm (and good tools), confident
that you will be able to find an answer quickly.
Try to balance action and checking.
Avoid the extremes of passive inactivity (because you're afraid to make a mistake?)
and unconstrained action (when you never check for correctness). One useful
strategy is the creative process of brainstorm-and-edit: first get ideas and
then decide whether they're "good" ideas. This is also
a good way to solve problems. Often, the hardest part of a solution is
just getting started; after brainstorming gets you moving, you can edit
the solution-plan and steer the movement in a useful direction.
PROCESS: In effective problem
solving there is overlap between the phases of orientation, planning, action
and checking. During orientation you search for a solution plan and check
it for correctness in quick brainstorm-and-edit cycles. And with go-and-improvise
you begin action before the entire strategy is planned.
Expert solution finders explore problems
with non-mathematical thought. During orientation they "play
with the problem", trying to fully understand its physical characteristics.
This is usually done by getting the big picture first and filling in
the details later. In "The Physics Teacher" of May 1981,
Fred Reif uses an art analogy to illustrate a "successive refinements"
orientation toward problem-solving process, by comparing two ways to paint a
woman's portrait:
"... One might begin by first painting
completely the woman's eye, then her eyebrow, then her nose, and so forth until
the entire portrait has been completed. The same problem might be approached
by a "method of successive refinements" which deals first with the
major features of the portrait and then successively with more minor features.
Thus one might begin by first drawing a rough sketch of the entire woman, then
elaborating this sketch by additional lines, and then successively elaborating
with more lines and colors until the entire portrait has been completed.
Almost any painter would use the second method. ... In scientific
problem solving, such a method of successive refinements can be implemented
effectively by using successively more detailed levels of description of the
same situation."
During a successive-refinements orientation,
an expert will often discover the equation that leads to a solution. This
occurs because he (or she) has good physical intuition, built on a solid
foundation of understanding and experience. Part of this intuition is
equation knowledge; if there is a clear mental picture of the connection
between a physical situation and the equations that describe it, understanding
the physical situation (by exploring the problem with non-mathematical thinking)
will naturally lead to the proper equation.
In contrast, beginners notice that equations are used
in most solutions, so their immediate goal is to find-an-equation. Too
much attention is focused on equations, the visible "tip of the iceberg," and
not enough on the "main body of the iceberg below the surface" — the
physical understanding that is needed to use equations wisely.
If you get stuck sometime during the solution, you'll have to decide
whether to continue in the direction you're going or to change course.
|
PERSEVERANCE is needed.
|
FLEXIBILITY is needed.
|
|

|
|
to help you keep moving in a useful direction.
Look for signs of toward-the-goal progress (or lack of it)
in the direction you're moving.
You may have a feeling, based on logic and experience,
that your solution strategy isn't working and probably never will.
Or you may feel that the goal is almost in sight and you'll soon reach it.
Checking Your Answer. To find
out whether you've reached the goal, ask:
Have I answered all of the questions that
were asked? Are my answers reasonable? Are the units correct?
If the correct answer is available (on a teacher's solution sheet or in the
back of the textbook), compare it with your answer.
You can also ask: Is there more than one
possible answer? { In science class there is often, but not always,
only one solution to a problem. But for many problems in life, and some
in science, there can be alternative solutions. }
Or you can ask: Is there more than
one method that will lead to the same answer?
Find The Trouble and Fix
It
A troubleshooter
is "an expert in discovering and eliminating the cause of trouble in mechanical
equipment." (Random House Dictionary)
You can do troubleshooting with ideas, too.
If you can't solve a problem, find what is causing the trouble and fix it.
Check the orientation: Have you correctly
interpreted all available information (written, visual and free) to get the
proper problem-situation? Do you know what questions are being asked?
What progress have you already made toward the goal? Where are you now,
and what still needs to be done? { Orientation is important.
When a student can't do a problem, I'll often just say "Read the problem
again; have you missed anything?" or "look at the picture",
and he can easily solve the problem on his own.}
Have you ignored any "cues" that
tell you to use a particular equation?
How certain are you of your overall solution
plan? Of the individual parts?
If you think the method is correct but you
didn't get a correct answer, check the details. Is the substitution, algebra
and arithmetic correct? Is everything in the correct units? Have
you done all of the necessary steps?
If all else fails, try dividing the correct
answer (if it is available) by your answer, or vice versa. If you can
recognize anything special about the division result [if it equals 10 raised
to some power, or 2 or 1/2 or 4 or..., or pi or 2 pi, or some constant of nature,
or...] this may give you a clue about what is wrong with your solution.
If you still can't solve the problem you
may be missing an essential tool. Re-read the appropriate part of your
textbook to search for this tool. Or ask someone for help: ask a fellow
student, or a tutor, T.A. or teacher.
But you may just need a change of pace.
Sometimes the best thing you can do is get away from the problem for awhile.
This option is discussed next.
INCUBATION — using "vacations" to
solve problems
If you stop work on an unsolved
problem and return to it later, you may quickly find the answer. Why?
a new approach: If you get stuck in an unproductive rut, it may
be easy to break loose (and move onto a better path) when time has weakened
the rut's hold on your thinking habits. an alert mind: If fatigue
has decreased your productivity, a break can restore the fresh, clear thinking
and confident attitude you need for success. new knowledge: Between
attempts, you may discover a key insight that lets you easily solve the problem
the next time you see it. subconscious thought: Even when you don't
actively work on a problem, thinking can still occur "under the surface
of your mind" and this may help you find a solution later.
Using an analogy between hatching eggs and
ideas, the waiting period between solution attempts is called incubation. Here are two useful tips:
1) To hatch ideas, you must give your mind
something to work with. The closer you come to a solution on your first
attempt, the more likely it is that you'll succeed on the second attempt or
third attempt or... The incubation process is ON-OFF-ON: active thought
(with solution as the goal), a break, then more active thought.
2) Expect an answer. When you take
a break, tell yourself "The next time I see this problem, I'll be able
to solve it."
Time: An incubation break can be short
or long, lasting minutes, hours, days, ...
Activities: You can skip to the next
problem, study another subject, lay down and rest, go for a run, do the dishes,
listen to music, talk with a friend, relax in isolated silence, sleep (think
about the problem when you wake up, before you get involved in other activities),...
Don't be lazy (or cowardly) by using incubation
as an excuse to procrastinate, to avoid a challenge you should face. But
don't waste time, either. If you're making progress, keep going!
If not, decide whether doing something else for awhile is a better use of your
time, or whether you should persevere.
how to LEARN MORE
from your problem-solving experience:
When you finish a problem, review
what you've done and, like the expert welder, ask: What can I learn from
this problem that will help me do better in the future?
If you solved the problem, ask: What
did I do, and why did it work?
If you initially had trouble but eventually
solved the problem, ask: What was wrong with my original approach?
Was my orientation incomplete or inaccurate? Did I lack skill in using
the necessary tools? How can I change my approach so the next time I see
a similar problem it will "look different" — more like it should
for inspiring a solution?
If you couldn't solve it, use the strategies
in "Troubleshooting" and "Incubation" above.
If possible, do problems with answers so
you have feedback. A correct answer gives you confidence, and a wrong
answer says "change what you're doing."
When you make a rough draft summary (as
described in Section 20.3) and use it for problem-solving practice, two good
things happen: 1) the summary improves your problem-solving skill, and
2) you'll discover ways to make the notes better so they can help improve your
skill even more.
Notice how each problem fits into the logical
organization of your summary notes and look for patterns: Do you recognize
any reoccurring sub-problem combinations? Can the summary's organization
be changed to show strategy relationships more clearly? Should any tools
(or suggestions for using them) be added to your notes? What will make
the notes more useful for your problem-solving needs?
Searching for insights and principles plus practice are discussed in Searching for Insight, using a skier and welder as examples. The diagram below shows the "levels of learning" interactions between specific strategies (like those in Chapters 1-19) and general strategies (as in Chapter 20): PRACTICE with "searching for insight" ANALYSIS helps you learn SPECIFIC STRATEGIES and GENERAL STRATEGIES, and also helps you combine both of these levels (as shown by the <--> ) into a flexible, powerful problem-solving system.
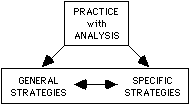
by mastering and using STUDY SKILLS and POWER TOOLS.
20.92 More Problem-Solving Strategies
Flexibility and Perseverance
Robert McKim, in his book "Experiences
in Visual Thinking," discusses the relative merits of perseverance and
flexibility: "When should you abandon one strategy to try another?
When is perseverance a virtue, and when is flexibility? Sometimes dogged
persistence in the use of a single strategy yields a solution: despite frustration
and fatigue, the thinker rattles the same key in the door until it opens.
On the other hand, it may simply be the wrong key. When staying with one
strategy pays off, we call it "perseverance"; when it does not,
we call it "stubborn inflexibility." Genius is often associated
with the ability to persevere or, in Edison's terms, to perspire. Creativity
is also linked to the ability to be flexible. Clearly, we are facing a
paradox. Perseverance and flexibility are opposites that together form
an important unity."
Playing with Problems
Modes of Thinking:
To be a good problem-solver, you must translate ideas fluently between three
modes of thinking: verbal, visual and mathematical.
I like to think of these modes more concretely, in terms of their most common
use in physics problems: words, pictures (on-paper or in-the-mind)
and equations:
Beginning students often try to translate directly from words
to equations. They have noticed that equations are used in most solutions,
so their immediate goal is to "find an equation." By contrast,
expert solution-finders explore a problem with non-mathematical thought, "playing
with the problem" until words have been translated into a clear, complete
mental picture of the physical situation, often by using a successive refinements
orientation that aims for getting the big picture first and filling in
the details later.
In the context of problem solving, "pictures"
is anything that helps you (1) form a clear idea of the problem situation,
and (2) bridge the gap between words and equations. This could be
a force diagram [drawn from a word-description, then used to substitute into
the F=ma equation] or a tvvax table [whose structure makes it easy to store
information so you can see what is "known" and "unknown"]
or an actual drawing, a mental image, or...
A picture-idea often leads to a useful equation.
This is why it is important to know the "physical meaning" of equations:
If you have a strong, clear idea of the connection between each equation and
the physical reality it represents, understanding a physical situation (by exploring
the problem with non-mathematical thinking) will naturally lead you to a true-and-useful
equation.
As emphasized in Section 2.3, PHYSICS MATH
is easy. It is the mastery of PHYSICS CONCEPTS that will make you a problem-solving
expert. { The main math we have so far is right-triangle trig (easy),
tvvax equations (easy), and F=ma (very easy), but problems can still be challenging
if they require that you interpret complex physical situations, or use ideas
that are not yet internalized-and-intuitive [for example, if you're still "fighting"
the independent analysis of x and y motion, it may be difficult to remember
this tool when you need it to solve a problem]. }
Even though math isn't the problem-solving
"key", it is important and shouldn't be ignored. In fact ,
one goal of this book is to help you be totally comfortable with math so your
mind is free to think about words and pictures. If you are confident about
coping with math, you can relax and focus your attention on physics!
DRAW TO PRODUCE LOGIC, NOT ART: When
you solve a physics problem, use drawing as a thinking tool, to help you translate
words into clear picture-ideas. Relax and let the ideas flow; aim
for logical creative thought, not "art".
The main ideas from Section 20.8, about productive thinking, are summarized
in another page.